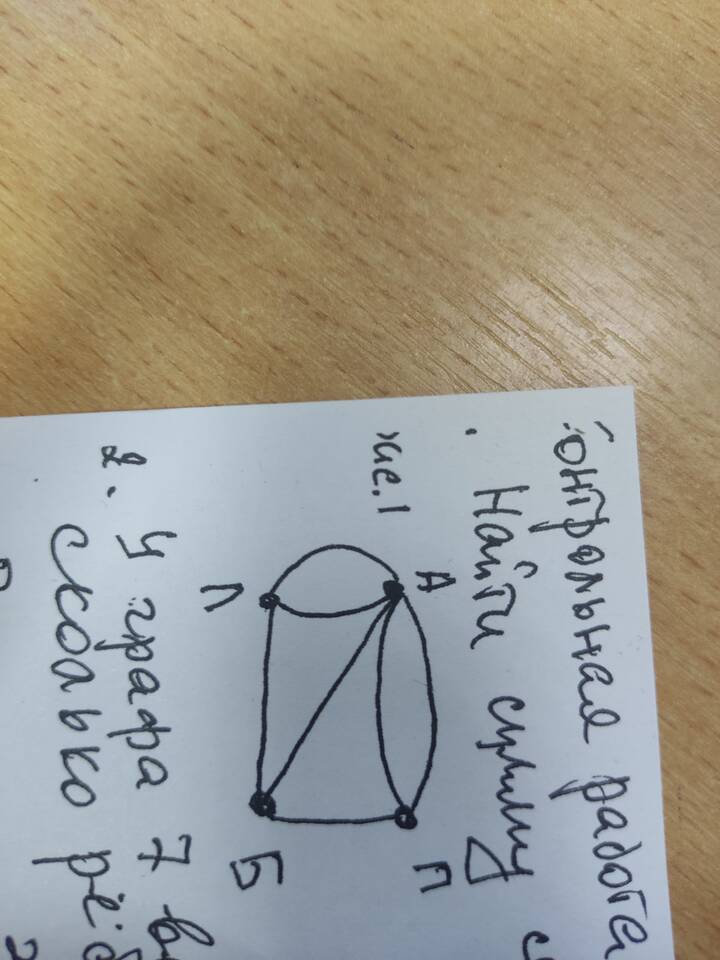
Сумма степеней графа - это сумма степеней всех его вершин. В теории графов это важная характеристика, которая имеет фундаментальное значение для анализа свойств графа.
Содержание
Основное определение
Формальное определение
Для графа G = (V, E), где V - множество вершин, а E - множество ребер, сумма степеней S вычисляется по формуле:
S = Σ deg(v) для всех v ∈ V
где deg(v) - степень вершины v (количество инцидентных ей ребер).
Основная теорема
| Теорема | Формулировка |
| Лемма о рукопожатиях | Сумма степеней всех вершин графа равна удвоенному количеству его ребер: S = 2|E| |
Следствия из теоремы
- Сумма степеней всегда четна
- Количество вершин с нечетной степенью всегда четно
- Средняя степень вершины равна 2|E|/|V|
Примеры вычислений
| Тип графа | Сумма степеней |
| Полный граф Kn | n(n-1) |
| Цикл Cn | 2n |
| Дерево с n вершинами | 2(n-1) |
| Двудольный граф Km,n | 2mn |
Применение суммы степеней
- Проверка корректности задания графа
- Определение существования графа с заданными степенями вершин
- Анализ связности графа
- Решение задач о существовании эйлеровых циклов
Алгоритм проверки
Чтобы проверить, может ли существовать граф с заданными степенями вершин:
- Убедитесь, что сумма степеней четна
- Проверьте, что для всех вершин deg(v) ≤ |V|-1
- Примените алгоритм Хавел-Хакими (для простых графов)
Связь с другими характеристиками
| Характеристика | Связь с суммой степеней |
| Количество ребер | Прямо пропорциональна (S = 2|E|) |
| Средняя степень | S/|V| |
| Минимальная степень | ≤ S/|V| |
| Максимальная степень | ≥ S/|V| |
Заключение
Сумма степеней графа - это фундаментальная характеристика, которая связывает количество вершин и ребер графа. Ее анализ позволяет делать важные выводы о структуре и свойствах графа, а также проверять корректность его задания.